Л . В. Канторович - математик и экономист

С. С.  Кутателадзе, В. Л.  Макаров

И. В.  Романовский, Г. Ш. Рубинштейн

To be published

Леонид Витальевич Канторович вошел в плеяду крупнейших ученых двадцатого века благодаря своему капитальному вкладу в математику и экономику. Исследования Л. В. Канторовича в области функционального анализа, вычислительной математики, теории экстремальных задач, дескриптивной теории функций и теории множеств оказали влияние на становление указанных математических дисциплин, послужили основой для формирования новых научных направлений.

Л. В. Канторович по праву считается одним из основоположников современного экономико-математического направления, ядро которого составляют теория и модели линейных экстремальных задач. Это направление было затем переоткрыто и развито в трудах других ученых (прежде всего Дж. Данцига) и получило название <<линейное программирование>>;. Идеи и методы этой дисциплины широко используются для постановки и решения разнообразных экстремальных и вариационных задач не только в экономике, но и в физике, химии, энергетике, геологии, биологии, механике и теории управления. Линейное программирование оказывает существенное влияние также на развитие вычислительной математики и вычислительной техники. Нам представляется, что никто другой не сделал так много для использования линейного программирования в экономической теории, как Л. В. Канторович.

Жизненный путь

По окончании ЛГУ в 1930  г. Леонид Витальевич преподавал в высших учебных заведениях Ленинграда, продолжая при этом активную научную деятельность. Из этих учебных заведений кроме Ленинградского университета назовем особо Высшее военное инженерно-техническое училище. В годы Великой Отечественной войны Л. В. Канторович был призван в Вооруженные Силы, и преподавание в этом училище было его основным делом. В это время он написал оригинальный курс <<Теория вероятностей>> (1946), предназначенный для военных учебных заведений и отражающий специфические военные приложения этой науки. Список трудов Л. В. Канторовича опубликован в  <<Математика в СССР за сорок лет, 1917-1957>>, т. II, с. 292; <<Математика в СССР, 1958-1967>>, т. 2, вып. 1, с. 568; УМН, 1972, 27:3, с. 225;УМН, 1982, 37:3, с. 206; УМН, 1987, 42:2, с. 180-182. См. также Материалы к биобиблиографии ученых СССР. Серия математических наук, вып. 18. М.: Наука, 1986. ИТУ, называемое теперь Военным инженерно-техническим университетом, до сих пор хранит память о Л. В. Канторовиче, и в 1999 г. по инициативе ВИТУ на его здании в Петербурге появилась мемориальная доска о нем.

С 1932  г. Л. В. Канторович работал в должности доцента ЛГУ и профессора в будущем ВИТУ, а с января 1934  г. после утверждения в этом звании ВАК стал профессором ЛГУ. В 1935  г. ему была присуждена ученая степень доктора физико-математических наук без защиты диссертации. Профессором ЛГУ Леонид Витальевич оставался до своего отъезда в Новосибирск, о чем пойдет речь ниже.

Вскоре после выхода в свет основополагающей монографии С.  Банаха <<Théorie des operations lineaires>> в Ленинградском университете начинает формироваться одна из первых отечественных школ по функциональному анализу. Уже в 1934  г. в цикле работ Л. В.  Канторовича были получены важные результаты по теории функционалов и операторов в банаховых пространствах, существенно дополняющие классические исследования И.  Радона.

В эти же годы Л. В.  Канторович выдвинул фундаментальную идею изучения общих пространств, наделенных структурой условно полной векторной решетки. Необходимость привлечения структуры порядка в функциональном анализе была осознана почти одновременно и рядом других математиков (Ф.  Рисс и несколько позже, М. Г.  Крейн, Г.  Биркгоф, Г.  Фрейденталь).

Особый вклад Л. В. Канторовича - выделение в тридцатые годы прошлого века класса упорядоченных векторных пространств, в которых каждое порядково ограниченное множество имеет точную верхнюю и точную нижнюю границы. Эти пространства обладают рядом принципиально важных специфических свойств, позволивших предложить мощные новые методы исследования функциональных объектов, в том числе и классических. Теория таких пространств - их называют теперь пространствами Канторовича или K-пространствами - стала одним из основных разделов функционального анализа. Теории K-пространств была посвящена монография <<Функциональный анализ в полуупорядоченных пространствах>>, написанная Л. В.  Канторовичем со своими учениками Б. З. Вулихом и А. Г. Пинскером и вышедшая в свет в 1950 году.

Исследования последней четверти прошлого века наглядно показали, что так называемые расширенные или универсально полные пространства Канторовича суть ничто иное, как изображения поля вещественных чисел в булевозначных моделях классической теории множеств Цермело - Френкеля. Таким образом, пространства Канторовича столь же неизбежны в математике как и множество вещественных чисел. В качестве любопытной иллюстрации отметим, что в связи с возникновением булевозначного анализа расширенные пространства Канторовича были заново переоткрыты в США под названием <<булевы линейные пространства>> спустя полвека после своего появления в работах Леонида Витальевича и его учеников.

Л. В.  Канторович стоял у истоков формирования современной вычислительной математики. Первые работы по приближенным методам конформных отображений, вариационным методам, квадратурным формулам, численным методам решения интегральных уравнений и уравнений в частных производных были выполнены Леонидом Витальевичем в начале 30-х годов, когда вычислительна математика еще не оформилась в самостоятельную научную дисциплину. Важную роль в становлении вычислительной математики сыграла монография Л. В.  Канторовича и В. И. Крылова <<Методы приближенного решения уравнений в частных производных>> (1936). Эта книга, в дальнейшем называвшаяся <<Приближенные методы высшего анализа>>, неоднократно переиздавалась, переведена на английский, немецкий, венгерский, румынский языки и до сих пор широко используется специалистами во всем мире.

Необходимость разработки современных эффективных численных методов анализа разнообразных задач прикладного характера особенно остро стала ощущаться в последние предвоенные и в военные годы. А в 1948  г. в связи с необходимостью выполнения важных прикладных расчетов Л. В.  Канторович возглавил созданный в Математическом институте им. В. А. Стеклова и расположенный в Ленинграде Отдел приближенных вычислений. Он понимал, что дальнейшая разработка численных методов должна базироваться на фундаментальных результатах теоретических разделов математики, и приступил к исследованиям в этом направлении.

Основные результаты этих исследований были обобщены им в работах 1947-1948  гг.: <<К общей теории приближенных методов анализа>>, <<О методе Ньютона для функциональных уравнений>>, <<Функциональный анализ и прикладная математика>>, удостоенных в 1949  г. Сталинской (Государственной) премии.

В начале 50-х годов по инициативе Л. В. Канторовича на математико-механическом факультете Ленинградского университета была организована первая в нашей стране специализация по вычислительной математике, а в дальнейшем и кафедра, которую первоначально возглавил его соавтор В. И. Крылов. Леонид Витальевич всегда подчеркивал значение функционального анализа как теоретической базы вычислительной математики. Поэтому среди сотрудников и выпускников созданных им кафедр вычислительной математики в ЛГУ и НГУ всегда было много специалистов аналитического профиля.

С работами по вычислительной математике связано непосредственное участие Л. В. Канторовича в развитии вычислительной техники. Он руководил конструированием новых вычислительных устройств, ему принадлежит ряд изобретений в этой области. Совместно с учениками он разрабатывал оригинальные принципы машинного программирования для численных расчетов и, что было в те годы совершенно необычайно, для проведения сложных аналитических выкладок.

В 1939  г. вышла небольшая брошюра Л. В.  Канторовича <<Математические методы организации и планирования производства>>, в которой зафиксировано открытие линейного программирования - направления, оказавшего большое влияние на развитие экономической науки. В этой работе Леонидом Витальевичем впервые давалась математическая постановка производственных задач оптимального планирования и предполагались эффективные методы их решения и приемы экономического анализа этих задач. Тем самым идея оптимальности в экономике была поставлена на прочный научный фундамент.

Л. В.  Канторович уже тогда считал необходимым продолжать исследования в следующих направлениях: 1) дальнейшее развитие алгоритмов линейного программирования и их конкретизация для отдельных классов задач; 2)  обобщение предложенных методов с целью изучения более широких классов экстремальных задач с ограничениями, включая нелинейные задачи и задачи в функциональных пространствах; приложение таких методов к экстремальным задачам математики, механики и техники; 3)  распространение новых методов экономического анализа отдельных производственных задач на общие экономические системы; приложение этих методов к задачам планирования и анализа структуры экономических показателей на уровне отрасли, региона и народного хозяйства в целом.

Опубликованная в 1951 г. книга <<Расчет рационального раскроя промышленных материалов>> (написанная с В. А. Залгаллером) отражает замечательный опыт авторов по использованию методов оптимальных расчетов в задачах промышленного раскроя в докомпьютерный период.

Некоторые исследования по первым двум направлениям Л. В. Канторовичем были выполнены еще в предвоенные годы.

Однако основные усилия он сосредоточил на развитии третьего направления. Уже в 1942  г. им был написан первый вариант капитальной монографии <<Экономический расчет наилучшего использования ресурсов>>. Эта работа настолько опережала время и настолько не соответствовала тогдашней политической экономии (обычно ее догматам, а иногда и сути), что ее публикация оказалась возможной только в 1959  г., когда некоторые из догматов оказалось возможным поколебать. Тогда пионерские идеи Л. В.  Канторовича были легализованы, получили некоторое признание и начали использоваться в экономической практике страны.

В 1959 г. и повторно в 1960 г. монография Л. В.  Канторовича <<Экономический расчет наилучшего использования ресурсов>> наконец-то увидела свет. В дальнейшем эта книга была переведена на английский, французский, японский, румынский, словацкий, польский, сербский, испанский языки. Одновременно Леонид Витальевич продолжал свои математические исследования, и в том же году вышла совместная с Г. П. Акиловым книга <<Функционимевшая анализ в нормированных пространствах>>, также имевшая несколько изданий и переводов и ставшая на долгие годы одним из математических бестселлеров.

В 1965  г. исследования Л. В.  Канторовича в области экономико-математических методов были удостоены Ленинской премии (вместе c активно поддержавшим его В. С. Немчиновым и пришедшим к аналогичным идеям из экономических соображений В. В. Новожиловым), а в 1975  г. Л. В.  Канторович вместе с американским экономистом Т.  Купмансом был отмечен Нобелевской премией по экономике с формулировкой <<за вклад в теорию оптимального использования ресурсов>>.

В 1957  г. было принято государственное решение о создании нового крупного научного центра на востоке страны - Сибирского отделения Академии наук. Л. В.  Канторович был в первой группе ученых, приглашенных для работы в Сибирском отделении. В 1958  г. он был избран членом-корреспондентом по Отделению экономики, а в 1964  г. - действительным членом Академии наук по Отделению математики.

В 1958-1960  гг. B. C. Немчинов и Л. В.  Канторович возглавляли Лабораторию по применению математических и статистических методов в экономических исследованиях и планировании Сибирского отделения.

В 1960 г. ленинградская группа лаборатории во главе с Л. В. Канторовичем переехала в Новосибирск и влилась в качестве Математико-экономического отделения в Институт математики Сибирского отделения, носящий теперь имя С. Л. Соболева.

Московская группа этой лаборатории стала ядром при создании Центрального экономико-математического института Академии наук, дала толчок к созданию групп в Московском государственном университете и в Госплане, а один из членов этой группы дошел до поста первого заместителя Министра экономики России. Много видных управленцев вышло впоследствии из стен ЦЭМИ.

Еще до переезда в Новосибирск под руководством Л. В. Канторовича в Ленинграде были развернуты исследования по теории и численным методам математического программирования: а также в области теории и практического использования моделей оптимального планирования. В частности, разработанные здесь оптимальные тарифы на такси были реализованы в масштабе страны и принесли большой экономический эффект. В эти же годы по инициативе Л. В. Канторовича на математическом и экономическом факультетах Ленинградского университета началась подготовка специалистов по применениям математики в экономике. Большую роль сыграло формирование так называемого <<шестого курса>>: наиболее способные выпускники экономического факультета ЛГУ были оставлены для дополнительного одногодичного обучения математике и ее экономическим приложениям, к ним присоединились некоторые выпускники прежних лет и группа экономистов из Москвы. Два московских участника этой группы, А. А. Анчишкин и С. С. Шаталин, стали впоследствии академиками.

С 1960 по 1970  г. Л. В.  Канторович был заместителем директора Института, а также заведующим кафедрой вычислительной математики Новосибирского университета. С момента основания <<Сибирского математического журнала>> до своей кончины Леонид Витальевич Канторович входил в состав редколлегии, определяя научное лицо журнала в области прикладного функционального анализа и математической экономики.

Математико-экономическое отделение, организованное Л. В. Канторовичем в Институте математики Сибирского отделения, было одним из первых коллективов, где проблемы применения математических методов в экономике стали решаться комплексно. Наряду с развитием теории оптимального планирования и экономических показателей большое внимание здесь уделяется изучению моделей экономической динамики и равновесия, исследованиям в области выпуклого анализа и теории экстремальных задач, разработке численных методов математического программирования, включая их реализацию на ЭВМ, а также апробации и внедрению разработанных моделей и методов в экономическую практику.

Л. В. Канторович в указанные годы вел большую научно-организационную работу. По его инициативе, в частности, проводились всесоюзные и международные конференции и совещания по применению математических методов в экономике, на математическом и экономическом факультетах Новосибирского государственного университета была организована подготовка специалистов в области экономической кибернетики.

В 1971  г. Л. В. Канторович был переведен на работу в Москву, где руководил сначала Проблемной лабораторией Института управления народным хозяйством ГКНТ, а с 1976  г. - Отделом системного моделирования научно-технического прогресса Всесоюзного научно-исследовательского института системных исследований. Все эти годы Л. В. Канторович являлся членом Государственного комитета по науке и технике, участником ряда других комитетов и министерств как член научно-технических и экспертных советов.

В настоящее время многочисленные ученики и последователи Л. В.  Канторовича успешно работают в различных областях современной математики и экономики, добиваясь значительных научных результатов.

Выдающиеся заслуги Л. В.  Канторовича были отмечены государством. Он награжден двумя орденами Ленина - в те годы наивысшей наградой страны, тремя орденами Трудового Красного Знамени, орденами <<Знак Почета>> и Отечественной войны II степени, многими медалями.

Л. В.  Канторович был членом ряда зарубежных академий и почетным доктором многих университетов, участвовал в работе международных научных обществ.

До последних своих дней Леонид Витальевич был полон творческих планов и активно работал над их претворением в жизнь. Уже в последние месяцы своей жизни, находясь в больнице, он продиктовал свои автобиографические заметки <<Мой путь в науке>>, опубликованные в <<Успехах математических наук>>. Л. В.  Канторович скончался 7 апреля 1986 г. в Москве и похоронен на Новодевичьем кладбище.

Дескриптивная теория функций и теория множеств

Первые работы Л. В.  Канторовича, доложенные на семинаре Г. М.  Фихтенгольца в 1927-1928  гг., посвящены исследованию трансфинитной последовательности классов функций, составляющих так называемую классификацию Янга. В этой классификации в качестве исходного принимается класс непрерывных функций, а последующие классы получаются чередованием предельных переходов возрастающих и убывающих последовательностей функций. Классификация Янга является детализацией классификации Бэра.

Л. В. Канторовичем установлено, что функции Янга класса (a+1) представимы как верхние и нижние пределы функций Бэра класса (a) <<Sur les suites des fonctions rentrant dans la classification de M. W. H. Young>> (1929). Ему принадлежат также построения универсальных функций для классов Янга: <<Об универсальных функциях>> (1929); функция двух переменных называется универсальной для данного класса, если при специализациях одной из переменных получаются все функции одной переменной этого класса. Универсальные функции Л. В.  Канторовича принадлежат тем же классам, что и представляемые ими функции. Для классификации Бэра, как показано Леонидом Витальевичем, такого рода универсальных функций не существует.

К тому же циклу относится работа 1932  г. <<Об обобщенных производных непрерывных функций>>, которая посвящена условиям существования непрерывной функции, у которой производные числа Дини совпадают со значениями заданных четырех функций соответствующих классов. Дана дескриптивная характеристика этих функций и множеств, с помощью которых решается задача. Например, на совершенном множестве меры нуль произвольная функция первого класса Бэра оказывается производной некоторой функции. Полученные Л. В. Канторовичем достаточные и частично необходимые условия существенно дополнили классические результаты А. Лебега, Р. Бэра, А.  Данжуа, У.  Янга и А.  Безиковича.

Принципиальные результаты по теории A-множеств и проективных множеств получены Л. В.  Канторовичем в работах, выполненных преимущественно в соавторстве с Е. М. Ливенсоном. Основными из них являются <<Memoir on the analytical operations and projective sets>> (1932, 1933). В этой серии работ развивается общая теория аналитических операций над множествами, в частности, теория ds-операций Хаусдорфа - Колмогорова. Под этим названием понимается операция F_N, сопоставляющая счетной системе множеств E₁,E₂,...,E_n,... множество

å g О N  En1En2... Enl=FN(E1,E2,...).

Здесь g = (n₁,n₂,...) - последовательность натуральных чисел, а N - множество последовательностей g, определяющее операцию. К ds-операциям относится, например, A-операция П. С.  Александрова, применение которой к замкнутым множествам порождает A-множества. Устанавливаются теоремы о зависимости дескриптивных свойств результата операции от класса множеств, из которого черпаются E₁, E₂, ... , а также от дескриптивных свойств множества N, рассматриваемого как множество иррациональных чисел.

В качестве одного из приложений построенной теории доказывается, что все трансфинитные последовательности так называемых C-множеств, получающихся применением A-операции к множествам, дополнительным к множествам предыдущего класса (за исходный класс берут A-множества), укладываются во второй проективный класс. Впервые дано также аналитическое представление всех проективных классов.

Конструктивная теория функций

К началу 30-х годов относятся также первые работы Л. В.  Канторовича по конструктивной теории функций. Его внимание в этой области привлекли прежде всего известные многочлены

Bn f(x)= n å k=0  f м о  k n ц ш Cnk xk(1-x)n-k,

с помощью которых С. Н. Бернштейн в 1912  г. дал оригинальное доказательство знаменитой теоремы Вейерштрасса. В статье <<О сходимости последовательности полиномов С. Н.  Бернштейна за пределами основного интервала>> (1931) Л. В.  Канторович установил следующий неожиданный факт: если функция f регулярна хотя бы на части отрезка (0,1), то сходимость B_n f к f имеет место в некоторой части комплексной области. Эти исследования Л. В.  Канторовича были продолжены С. Н.  Бернштейном в нескольких работах 1936-1943  гг.

В статье <<О некоторых разложениях по полиномам в форме С. Н.  Бернштейна>> (1930) Л. В.  Канторович заметил, что запись произвольного многочлена P_n степени n в форме

Pn(x)= n å k=0  j(n)kCnkxk(1-x)n-k

может оказаться весьма полезной,

jk(n)=(n+1) (k+1)/(n+1) у х k/(n+1)  f(t)dt,

Леонид Витальевич нашел сингулярный интеграл, сходящийся к соответствующей функции f О L[0,1] почти везде. Это позволяет доказать почленную дифференцируемость почти везде последовательности полиномов Бернштейна для абсолютно непрерывной функции f.

Используя другой выбор j_k⁽ⁿ⁾, Л. В.  Канторович получил простое доказательство известной теоремы Бэра о представлении полунепрерывной функции в виде предела монотонной последовательности непрерывных функций. В более поздней работе <<Об общих методах улучшения сходимости в способах приближенного решения граничных задач математической физики>> (1934 г.) на основе еще одного выбора j_k⁽ⁿ⁾ Леонид Витальевич создал аналитический аппарат для представления произвольной измеримой функции во всех ее точках аппроксимативной непрерывности. Этот аппарат до сих пор используется в теории функций.

К рассматриваемому циклу относится также стать <<Несколько замечаний о приближении к функциям посредством полиномов с целыми коэффициентами>> (1931), в которой решается задача существенности ухудшения наилучшего приближения непрерывной функции многочленами, если потребовать, чтобы коэффициенты таких многочленов были целыми. Эти исследования были продолжены А. О.  Гельфондом в 1955  г.

Приближенные методы анализа

Первые работы Л. В.  Канторовича по приближенным методам анализа были опубликованы в 1933  г.

В 1933-1934 гг. им предложено несколько методов приближенного решения задачи о конформном отображении круга на односвязную область, ограниченную некоторой кривой. Эти методы основаны на погружении заданной области в однопараметрическое семейство, включающее область, для которой конформное отображение известно. Используя затем разложение по малому параметру, Леонид Витальевич вывел явные формулы для приближенного вычисления искомого конформного отображения <<О конформном отображении многосвязных областей>> (1934).

Дальнейшему развитию этого подхода и его обобщению на случай многосвязных областей посвящены работы 1933-1938 годов. Предложенный Леонидом Витальевичем метод малого параметра уже в 1933  г. был включен В. И.  Смирновым в третий том его учебника <<Курс высшей математики>>. Этот метод широко используется в механике, а также в работах Г. М.  Голузина по экстремальным проблемам теории функций.

В работе <<Один прямой метод решения задачи о минимуме двойного интеграла>> (1933) был предложен новый вариационный метод приближенного решения двумерных уравнений эллиптического типа, основанный на сведении соответствующей задачи минимизации интеграла

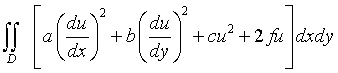
на множестве функций двух переменных к минимизации функционала, зависящего от нескольких функций одного переменного (метод приведения к обыкновенным дифференциальным уравнениям). Этот метод Л. В. Канторовича вошел в руководства по математике (Л. Э.  Эльсгольц) и механике (А. И.  Лурье).

Дальнейшему развитию вариационного метода, а также других приближенных методов решения дифференциальных интегральных уравнений посвящены работы 1934-1937  гг.

В частности, в статье <<Применение интеграла Стилтьеса к расчету балки, лежащей на упругом основании>> (1934) был впервые предложен известный метод коллокации. Указанные методы до сих пор широко используются в приложениях - механике, технике и физике.

К рассматриваемому циклу примыкают также исследования Л. В.  Канторовича по методу Ритца. В них дается ряд теорем о сходимости, а также методы приведения к обыкновенным дифференциальным уравнениям, основанные на сочетании идей конструктивной теории функций с аналитической техникой оценок операторов. Этими вопросами в то время, как известно, занимались Н. М.  Крылов, Н. Н.  Боголюбов, Г.  И.  Петров, М. В.  Келдыш и другие. Исследования Л. В.  Канторовича получили дальнейшее развитие в работах его учеников.

В теории механических квадратур Л. В.  Канторович, мастерски используя простую идею об аддитивном выделении особенностей, привел в статье <<О приближенном вычислении некоторых типов определенных интегралов и других применениях метода выделения особенностей>> (1934) ряд остроумных приемов для вычисления интегралов от гладких функций. Это послужило также источником построения численных методов решения интегральных уравнений при наличии сингулярностей, в частности, уравнений теории переноса.

В более поздней работе <<Об особых приемах численного интегрирования четных и нечетных функций>>(1949) выводятся формулы численного интегрирования четных и нечетных функций, которые при n узлах дают точные результаты для полиномов до степени 4n-2. Отсюда получаются и некоторые кубатурные формулы.

Разработанные Л. В.  Канторовичем методы отражены в монографии 1936  г., написанной им совместно с В. И.  Крыловым, <<Методы приближенного решения уравнений в частных производных>> (2-е изд. - <<Приближенные методы высшего анализа>>, 1941  г.).

Это сочинение стало первой в мировой научной литературе книгой по численным методам высшего анализа, неоднократно переиздававшейся в дальнейшем в нашей стране и за рубежом.

Функциональный анализ

Выполненные в 1934  г. работы Л. В.  Канторовича и Г. М.  Фихтенгольца по проблеме представления линейных функционалов и операторов явились первыми исследованиями российских математиков по теории нормированных пространств. В то время функциональный анализ еще только оформлялся в самостоятельное научное направление, и одной из первостепенных задач было накопление фактического материала - осмысление общих понятий в конкретных ситуациях. Поскольку основой всех построений функционального анализа того времени служили нормированные пространства и линейные операторы в них, большое значение приобретало аналитическое представление линейных функционалов и операторов в конкретных нормированных пространствах. К 1934  г. общая форма линейного функционала была известна для всех классических банаховых пространств, за исключением пространства L_∞ всех ограниченных измеримых функций. Иначе обстояло дело с аналитическим представлением операторов. Результаты И.  Радона (общие формы ограниченных и компактных операторов из пространства C непрерывных функций в себя) были единственными значительными результатами в этом направлении. Полученные Л. В.  Канторовичем и Г. М.  Фихтенгольцем теоремы об общем виде линейных функционалов и об аналитическом представлении ограниченных операторов, действующих из C в L_∞, заполнили имевшиеся пробелы в списке известных сопряженных пространств и послужили отправным пунктом для дальнейших исследований по теории линейных операторов. Отметим, что в работе <<Некоторые теоремы о линейных функционалах>> (1934) на основе полученных результатов установлена недополняемость пространства C в L_∞, что представляет интерес с точки зрения современной геометрической теории банаховых пространств. В этой же работе дано также решение проблемы Банаха о мощности множества линейных функционалов в пространстве M ограниченных функций.

К тому же периоду относятся исследования Л. В. Канторовича, посвященные одной из наиболее актуальных проблем 30-х годов - развитию математического аппарата, используемого в физике и квантовой механике. Леонид Витальевич поставил задачу <<распространения - <<обогащения>> функционального пространства Гильберта за счет введения <<идеальных>> функций, которые уже не будут функциями в обычном смысле>>. Существенно новым по сравнению с исследованиями К. Фридрихса здесь явилась предложенная Л. В.  Канторовичем схема пополнения, основанная на рассмотрении не одного, а целого семейства самосопряженных плотно определенных операторов, связанных с операторами дифференцирования. Этот же круг вопросов - обобщенные функции и решения - был затронут в его работах об обобщенных интегралах Стилтьеса.

В середине 30-х годов прошлого века в исследованиях Леонида Витальевича создавалось новое важное направление функционального анализа - теория упорядоченных пространств. Л. В.  Канторович вводил и подробно изучал класс векторных решеток, в которых всякое ограниченное множество элементов имеет точные границы (такие пространства, как уже отмечалось, вошли в литературу под названием K-пространства). Большое внимание Леонид Витальевич уделял регулярным K-пространствам, где сходимость по упорядочению обладает рядом свойств, сближающих ее с обычной сходимостью в множестве вещественных чисел. Леонид Витальевич строил теорию операторов в K-пространствах, выделяя в качестве основного класс регулярных операторов, т. е. таких линейных операторов, которые представимы в виде разности двух положительных линейных операторов. Он доказал, что совокупность регулярных операторов, отображающих одно K-пространство в другое, также образует K-пространство (<<О некоторых классах линейных операций>>, 1936). Этот результат представляет собой далеко идущее обобщение теоремы Ф.  Рисса, относящейся к конкретному пространству функционалов.

Параллельно с разработкой общей теории K-пространств Леонид Витальевич дал разнообразные приложения этой теории ко многим вопросам функционального анализа, теории функций и теории функциональных уравнений. Поскольку многие классические функциональные пространства, изучавшиеся методами теории нормированных пространств, оказываются одновременно K-пространствами, то привлечение к изучению таких функциональных пространств теории K-пространств позволило Л. В.  Канторовичу провести более детальное исследование линейных операторов. Леонид Витальевич (частично совместно с Б. З.  Вулихом) установил общие аналитические представления линейных операторов различных классов во многих конкретных пространствах. Теоремы Канторовича о распространении операторов нашли в его работах применения к теории интеграла, меры, а также к решению положительной проблемы моментов. Из общих соображений Леонидом Витальевичем были получены аналоги теорем Гамбургера, Стилтьеса и Хаусдорфа. Теоремы о сходимости последовательностей линейных операторов в K-пространствах Л. В.  Канторович применил к теории неопределенного интеграла Лебега и к теории ортогональных рядов.

Для приложений функционального анализа к теории численных методов оказалась чрезвычайно полезной построенная Л. В.  Канторовичем теория пространств, нормированных в обобщенном смысле - с помощью элементов некоторого K-пространства. Такие обобщенно нормированные пространства называют теперь решеточно-нормированными или B_K-пространствами. В теорию B_K-пространств включается и теория самих K-пространств (в этом случае в роли нормирующего пространства выступает то же самое K-пространство) и теория нормированных пространств (нормирующее пространство - поле вещественных чисел). Для B_K-пространств Леонид Витальевич получил ряд теорем о методе последовательных приближений. Эти теоремы используются при анализе численных методов решения конечных и бесконечных систем уравнений, в том числе линейных и нелинейных дифференциальных, а также интегральных уравнений. Одновременно этот подход позволил дать абстрактную трактовку классического метода мажорант: <<О функциональных уравнениях>> (1937). За указанный цикл работ в области теории упорядоченных векторных пространств Л. В.  Канторовичу на Первом всесоюзном конкурсе работ молодых ученых (1938) была присуждена первая премия. В восьмидесятые годы прошлого века в рамках булевозначного анализа было доказано, что решеточно-нормированные пространства Канторовича, удовлетворяющие введенной им специальной аксиоме разложимости нормы, служат изображениями обычных банаховых пространств. Поучительно, что аксиома разложимости нормы часто исключалась учениками Канторовича в последующих исследованиях как имеющая непонятную природу. Время подтвердило прозорливость Леонида Витальевича: на современном языке разложимость нормы оказывается эквивалентной переформулировкой ее экстенсиональности.

В 1940  г. Л. В.  Канторович приступил к подготовке итоговой монографии. Однако работа над этой монографией была завершена совместно с Б. З.  Вулихом и А. Г.  Пинскером лишь к концу 40-х годов прошлого века. В книге <<Функциональный анализ>> в полуупорядоченных пространствах>> (1950) впервые дается систематическое изложение теории K-пространств. Она до сих пор является ценным пособием для специалистов в этой области. Некоторым дополнением к ней является обзорная стать <<Полуупорядоченные группы и линейные полуупорядоченные пространства>> (1951).

Прогресс математики и расширение сферы ее приложений подтвердили значимость теории K-пространств, которая стала одним из основных разделов функционального анализа.

Л. В. Канторович постоянно подчеркивал неразрывную связь теории K-пространств с теорией неравенств и экономической проблематикой. Последующие исследования многих авторов подтвердили, что идеи линейного программирования имманентны теории K-пространств в следующем строго математическом плане: выполнение в абстрактной математической структуре любого из принятых вариантов формулировок принципа двойственности с  неизбежностью приводит к тому, что исходный объект является K-пространством.

Удивительно прозорливым оказалось многократно высказанное Л. В. Канторовичем положение о том, что элементы K-пространства суть обобщëнные числа. Эвристический принцип Канторовича, состоящий в том, что элементы K-пространства суть своего рода вещественные числа, нашëл блестящее подтверждение в рамках современной математической логики.

Развитие булевозначных моделей теории множеств, вызванное к жизни в 60-е годы прошлого века в в связи с решением проблемы континуума, продемонстрировало фундаментальное значение расширенных (универсально полных) K-пространств, каждое из которых, как неожиданно оказалось, служит новой равноправной моделью вещественной прямой. При этом решеточно-нормированные B_K-пространства, считавшиеся искусственными абстракциями, оказались в точности новыми изображениями обычных банаховых пространств. Тем самым K-пространства навсегда вошли в сокровищницу мировой науки.

Статья <<Приближенное решение функциональных уравнений>> (1956) связана с кругом идей С. Л. Соболева, использованных им в фундаментальных трудах по теоремам вложения различных функциональных классов. Отталкиваясь от своих исследований по аналитическому представлению операторов, Л. В.  Канторович предложил новую схему получения теорем вложения. Основой этой схемы является выделение нового важного класса ядер, обеспечивающего компактность соответствующих интегральных операторов. Выделенные ядра, именуемые ядрами Канторовича, широко используются в современной теории операторов.

С помощью идей из работы <<О перемещении масс>> (1942), связанных с рассмотрением транспортной задачи Л. В.  Канторович и Г. Ш.  Рубинштейн в 1958 г. предложили новую нормировку конечных мер на метрическом компакте. В полученном нормированном пространстве сильная сходимость при условии равномерной ограниченности полных вариаций оказывается эквивалентной обычной *-слабой сходимости соответствующих мер. Сопряженным к построенному пространству является пространство функций, удовлетворяющих условию Липшица. Благодаря этим свойствам указанное функциональное пространство (его называют пространством Канторовича - Рубинштейна) широко используется в приложениях, в частности в математической экономике и теории вероятностей.

В 1959  г. выходит монография <<Функциональный анализ в нормированных пространствах>>, написанная Л. В.  Канторовичем совместно с Г. П.  Акиловым. Эта монография оказала существенное влияние на исследования по применениям функционального анализа и на его преподавание в ведущих вузах страны и за рубежом. Наряду с оригинальной трактовкой традиционных разделов функционального анализа в нормированных пространствах большое внимание в книге уделено приложениям к вычислительной математике. Указанна монография переведена на многие языки. В 1977  г. вышло ее второе, существенно переработанное и дополненное издание (<<Функциональный анализ>>), в которое включены вопросы функционального анализа, связанные с математической экономикой, а также излагаются основы теории упорядоченных пространств. Это издание также переведено на несколько языков.

Функциональный анализ и прикладная математика

Л. В.  Канторович впервые применил функционально-аналитические методы в вычислительной математике. Этому направлению посвящены его работы 1937-1957  гг. Центральной здесь является статья <<Функциональный анализ и прикладная математика>> (1948), объединяющая целый цикл его работ и удостоенная Государственной премии. Само название этой статьи звучало в 1948  г. непривычно. Лишь теперь, причем в значительной степени благодаря работам Л. В. Канторовича, функциональный анализ стал основным аппаратом в исследованиях по вычислительной математике.

Основная мысль статьи заключается в том, <<что идеи и методы функционального анализа могут быть использованы дл построения и анализа эффективных практических алгоритмов математических задач с таким же успехом, как для теоретического анализа этих задач>>. С этих рассматриваются три вопроса: общая теория приближенных методов решения функциональных уравнений, метод наискорейшего спуска и функционально-аналитический вариант метода Ньютона.

Первая попытка объединения различных приближенных методов на основе изучения функциональных уравнений была предпринята Л. В.  Канторовичем еще в 1937  г. в работе <<О функциональных уравнениях>>. Ядром теории, предложенной в статье 1948  г. <<К общей теории приближенных методов анализа>>, явилась принципиально новая идея - изучение связи исследуемого функционального уравнения

Kx=y   (x О X, y О Y)

в банаховых пространствах X и Y с <<приближенным>> уравнением

~ K   ~ x   = ~ y      ( ~ x   О ~ X   ,  ~ y   О ~ Y   )

в более простых, как правило, конечномерных пространствах

Построенная Леонидом Витальевичем общая теория функциональных уравнений, базирующаяся на вариации исходных функциональных пространств и операторов, использовалась им для анализа основных приближенных методов решения важнейших классов уравнений второго рода (метод редукции для бесконечных систем линейных уравнений, различные методы решения интегральных и дифференциальных уравнений).

Получаемые при этом оценки оказывались, как правило, лучшими, чем ранее известные для соответствующих методов. Относительно некоторых методов теоремы сходимости и оценки скорости сходимости были установлены впервые, например для метода коллокации. Построенная Л. В. Канторовичем абстрактная теория приближенных методов сыграла важную роль в разработке и развитии разностных методов (B. C. Рябенький, А. Ф.  Филиппов), в ряде конкретных прикладных исследований (B. C. Владимиров, А. И.  Каландия и др.).

Общий метод наискорейшего спуска сформулирован Леонидом Витальевичем в работе <<Об одном эффективном методе решения экстремальных задач для квадратичных функционалов>> (1945), результаты которой были доложены им на семинаре в Математическом институте им. В. А. Стеклова еще в сентябре 1943 г. Этот метод в его простейшем варианте предназначен для решения линейных уравнений с положительно определенными операторами в гильбертовых пространствах. Л. В.  Канторовичем были установлены сходимость метода и точные оценки скорости сходимости. В настоящее время выяснены многочисленные связи метода наискорейшего спуска (в особенности его многошагового варианта) с другими методами решения задач линейной алгебры.

Работы Л. В. Канторовича по операторным уравнениям <<О методе Ньютона для функциональных уравнений>> (1948), <<О методе Ньютона>> (1949) блестяще подтверждают неоднократно выдвигавшиеся им два тезиса. Первый из них заключается в том, что разумно проведенное обобщение позволяет яснее увидеть существо дела и получить, как это ни парадоксально, более точный результат, чем при индивидуальном изучении частной задачи. Второй тезис состоит в том, что наличие хорошего приближения помогает не только локализировать предполагаемое решение, но и установить сам факт его существования.

Разработанный Леонидом Витальевичем функционально-аналитический вариант метода Ньютона принято называть методом Ньютона- Канторовича. В работах <<Принцип мажорант и метод Ньютона>> (1951), <<Некоторые дальнейшие применения метода Ньютона для функциональных уравнений>> (1957) Л. В.  Канторович дал более глубокую разработку общего метода мажорант, основанную на теории упорядоченных векторных пространств.

Линейное программирование

В 1938  г. к Л. В.  Канторовичу обратились сотрудники Центральной лаборатории Ленинградского фанерного треста с просьбой рекомендовать численный метод для расчета рационального плана загрузки имеющегося оборудования. Речь шла о комплексном выполнении пяти видов работ на лущильных станках восьми типов. Вопрос сводился к определению матрицы (h_ik) и величины z из условий

hik >= 0,    5 å k=1  hik=1,    8 å i=1  hikaik=zpk,   z→ max ,

где h_ik - суммарная производительность станков i-й группы при выполнении работ k-го вида, a p_k характеризует требуемый ассортимент. Из соответствующих результатов классического анализа вытекает, что в искомой матрице (h_ik) лишь двенадцать элементов отличны от нуля. Однако перебор всех таких комбинаций был сопряжен с непреодолимыми вычислительными трудностями (требовалось решить C¹²₄₀ ╩ 10⁹ систем линейных уравнений с двенадцатью неизвестными). Поэтому стало ясно, что эффективные методы решения подобных задач должны базироваться на принципиально новых идеях, позволяющих проводить целенаправленный перебор указанных комбинаций.

Ядром открытия Л. В.  является установленная им объективная связь задачи оптимального планирования с задачей определения соответствующих стоимостных показателей. На этой основе формулируются признаки оптимальности, позволяющие предложить различные схемы направленного перебора допустимых планов и систем стоимостных показателей. В частности, для приведенной задачи фанерного треста соответствующий признак состоит в следующем. Для оптимальности допустимого плана (h^*_ik) необходимо и достаточно, чтобы нашлись разрешающие множители l^*_k, удовлетворяющие соотношениям

l*k >= 0,    5 å k=1  l*k > 0,   l*kaik= max i  l*sais    при h*ik > 0.

Указанные разрешающие множители l^*_k объективно оценивают трудоемкость выполнения работ, а величины m^*_i=max_sl^*_sa_is можно рассматривать как прокатные оценки соответствующей группы станков.

Основам теории оптимального производственного планирования были посвящены доклады Л. В. Канторовича, с которыми он выступал в ЛГУ и Ленинградском институте инженеров промышленного строительства в мае 1939  г. В том же году была издана брошюра <<Математические методы организации и планирования промышленного производства>>, представляющая собой дополненную стенограмму этих докладов. В этой работе на основе разрешающих множителей исследуются различные классы планово-производственных задач.

Для характеристики широты охвата материала достаточно перечислить наименования разделов: распределение обработки деталей по станкам; организация производства с обеспечением максимального выполнения плана при условии заданного ассортимента; наиболее полное использование механизмов; максимальное использование комплексного сырья; наиболее рациональное использование топлива; рациональный раскрой материалов; наилучшее выполнение плана строительства при данных строительных материалах; наилучшее распределение посевных площадей; наилучший план перевозок. Математическому изложению и обоснованию предложенных методов посвящены три приложения. В последнем из них на основе геометрической интерпретации задач линейного программирования доказывается существование разрешающих множителей.

Выдающийся американский специалист в области линейного программирования Дж.  Данциг отмечал:

<<Работа Л. В.  Канторовича 1939  г. содержит почти все области приложений, известные в 1960  г.>> Данциг Дж. Б. Линейное программирование, его применение и обобщения: Пер. с англ. М., 1966. С.  29.Дальнейшему развитию и конкретизации методов линейного и нелинейного программирования посвящены многие работы Леонида Витальевича 1940-1981 гг.

Особый интерес представляет стать <<Об одном эффективном методе решения некоторых классов экстремальных проблем>> (1940), посвященная исследованию бесконечномерных задач выпуклого программирования. Для таких задач устанавливается признак оптимальности и формулируются идеи построения численных методов на основе последовательного улучшения имеющихся приближений. В ней дается характеристика не только решений оптимизационных задач, но и всех экстремальных или эффективных по Парето точек.

Большое внимание Л. В.  Канторович уделял исследованию специальных классов задач линейного программирования.

В 1940  г. Л. В.  Канторович и М. К. Гавурин изучили транспортную задачу в матричной и сетевой постановках. Предложенный ими метод потенциалов и его обобщение до сих пор широко используются в экономической практике. Бесконечномерный аналог транспортной задачи, исследованный в работе <<О перемещении масс>> (1942), позволил Л. В. Канторовичу в статье <<Об одной проблеме Монжа>> (1948) доказать справедливость известной гипотезы Монжа для широкого класса задач перемещения массы. На этой же основе, как уже отмечалось, построено и пространство Канторовича - Рубинштейна, широко используемое теперь в математической экономике и теории вероятностей.

Вопросам рационального раскроя посвящены работы Л. В.  Канторовича: <<Рациональные методы раскроя металла>> (1942); <<Подбор поставов, обеспечивающих максимальный выход пилопродукции в заданном ассортименте>> (1949), а также написанная им совместно с В. А.  Залгаллером монография <<Расчет рационального раскроя промышленных материалов>> (1951; 2-е изд. <<Рациональный раскрой промышленных материалов>>, 1971). Предложенные в монографии методы решений задач рационального раскроя наряду с алгоритмами линейного программирования используют оригинальные идеи вычисления индивидуальных раскроев. Аналогичные идеи были впоследствии развиты Р. Беллманом в теории динамического программирования.

Вычислительная техника и программирование

Л. В.  Канторович внес значительный вклад в развитие вычислительной техники и программирования.

Предложенные им алгоритмические и структурные решения легли в основу ряда оригинальных вычислительных устройств. В середине 50-х годов прошлого века под руководством Леонида Витальевича. были разработаны релейные клавишные вычислительные машины <<Вильнюс>> и <<Вятка>>, которые сыграли важную роль в автоматизации вычислительных работ на предприятиях и в учреждениях страны (<<Релейная клавишная вычислительная машина для автоматического выполнения арифметических операций>> (1959).

Интересные идеи, связанные с усовершенствованием различных десятичных вычислительных устройств, предложены в работах <<Устройство для умножения>> (1973); <<Электромеханическое запоминающее устройство>> (1974). В те же годы Л. В.  Канторович обратился к вопросам автоматизации программирования, а также других форм интеллектуальной деятельности человека (осуществление выкладок с символами, преобразование программ и т.п.). Предложенные им принципы (<<Об одной математической символике, удобной при проведении вычислений на машинах>> (1957) получили продолжение в ряде работ отечественных и зарубежных авторов.

Уже в начале 60-х годов прошлого века Л. В.  Канторович выдвинул идею <<усиления>> вычислительных возможностей универсальных ЭВМ путем комплексирования их со специализированными процессорами (приставками), ориентированными на массовые вычисления, характерные для того или иного класса задач.

В 1963-1965  гг. в Институте математики Сибирского отделения под руководством Л. В.  Канторовича был разработан специализированный процессор (<<Вычислительная система, состоящая из универсальной цифровой вычислительной машины и малой вычислительной машины>> (1965). В этой машине был использован предложенный Леонидом Витальевичем роторный принцип реализации массовых арифметических операций. Операции выполнялись с предельной скоростью, ограниченной только быстродействием оперативной памяти. Некоторые архитектурные решения, положенные в основу арифметической машины (прямой доступ к оперативной памяти, конвейерная организация обработки и др.), впоследствии получили широкое распространение в отечественных и зарубежных машинах. Использование проблемно-ориентированных процессоров считается сейчас одним из наиболее перспективных направлений развития вычислительных систем.

Заслуживают внимания также общие идеи Л. В. Канторовича о комплексном развитии машинной математики (методы, алгоритмы, программирование, структура машин): <<Комплексный подход к реализации массовых вычислений>> (1974).

Оптимальное планирование и оптимальные цены

Л. В.  Канторович заложил фундамент современной теории оптимального планирования. Развернутому изложению основных идей этой теории посвящена его капитальная монография <<Экономический расчет наилучшего использования ресурсов>> (1959, 1960). Стержнем этой книги является формулировка основной задачи производственного планирования и динамической задачи оптимального планирования. Указанные задачи достаточно просты, но в то же время учитывают важнейшие черты экономического планирования. Одно из привлекательных качеств состоит в том, что они базируются на схеме линейного программирования и, следовательно, на развитом аналитическом аппарате и обширном наборе эффективных вычислительных средств, часть из которых предложил сам Леонид Витальевич.

Динамическую задачу оптимального планирования Л. В.  Канторович формулирует следующим образом. Заданы наборы вещественных чисел

(askit)    s О S, (k,i,t) О N=K×I×T, (bkit)(k,i,t) О N0,

где K, I, T - конечные множества индексов, а N₀ - некоторое собственное подмножество множества  N. Требуется найти набор чисел (x^s), s О S, удовлетворяющий двум условиям:

1) å_{s О S}a^s_kit >= b_kit,    (k,i,t) О N₀,

2) не существует набора (^~x^s), s О S, удовлетворяющего  1) и неравенствам

å s О S  askit ~ x   s   >= å askitxs,    (k,i,t) О N\N0,

среди которых имеются строгие.

Содержательно набор чисел (a^s_kit) (k,i,t) О N₀ при фиксированном s О S интерпретируется как производственный способ по переработке одних ингредиентов в другие, где положительные числа означают выпуск, а отрицательные - затраты соответствующих продуктов k в пунктах или районах i в периоды времени t. Требуется найти такой производственный план, определяемый объемами (интенсивностями) x^s использования различных способов, при котором выполняются ограничения по ресурсам (b_kit > 0) и обеспечивается выполнение плановых заданий (b_kit < 0) и при этом не существует аналогичного плана (^~x^s), использующего меньшие ресурсы по всем (k,i,t) О N\N₀. Условие  2) обычно конкретизируется в зависимости от принятого критерия оптимальности.

Динамическая задача оптимального планирования привлекала большое внимание Л. В.  Канторовича и в последующие годы. В частности, ее дальнейшему развитию посвящена ключевая работа <<Динамическая модель оптимального планирования>> (1964); см. также <<Оптимальные модели перспективного планирования>> (1965). Здесь указаны важнейшие направления расширения и совершенствования основной схемы динамический модели и намечены пути использования ее в практике планирования. В этой работе Леонид Витальевич показал, как в экономическую модель вводятся элементы нелинейности, стохастики и дискретности и какую роль они играют как в более точном учете экономической реальности, так и при математическом анализе соответствующих моделей. Работа 1964  г., по существу, определила направление многих экономико-математических работ, которые были выполнены в последующие годы. За рубежом, в частности, большое развитие получило направление, именуемое теорией экономики благосостояния.

Все основные элементы этого направления заложены в работах Леонида Витальевича по глобальным оптимизационным моделям экономики. Выдающимся достижением Л. В.  Канторовича явилась формулировка оптимальных цен, осознание того факта, что цены и план составляют единую неразделимую систему и не могут рассматриваться изолированно. Указанные цены Леонид Витальевич назвал объективно-обусловленными оценками, чтобы подчеркнуть, что эти цены отражают совокупность условий, при которых составляется оптимальный план (отметим, что окончательное название было выбрано, когда велась уже корректура книги <<Экономический расчет>>, Леонид Витальевич заменил этим названием предыдущее <<наиболее целесообразные оценки>>, чтобы повысить <<критикоустойчивость>> термина).

В настоящее время общепринято, что объективно-обусловленные оценки оптимального плана - ориентир, к которому должны приближаться реальные цены.

Система объективно-обусловленных оценок включает в себя не только оценки обычных продуктов, но также оценки вкладов ресурсов, в том числе трудовых, оценки фондов, условий социального характера, оценки времени как фактора производства. Предложенный в этих работах подход к оценке природных ресурсов, <<прокатные>> оценки для оборудований прочно вошли в арсенал экономических показателей.

Своей трактовкой объективно-обусловленных оценок Л. В.  Канторович заложил основы оптимизационного экономико-математического анализа широкого круга фундаментальных экономических проблем, таких, как проблемы эффективности капитальных вложений, новой техники и других хозяйственных мероприятий, проблемы хозяйственного расчета, экономической оценки природных ресурсов, рационального использования труда.

Использование объективно-обусловленных оценок обеспечило существенное продвижение в проблеме выбора показателей оценки деятельности предприятий и других хозяйственных органов.

Следует заметить, что формулировка динамической модели оптимального планирования создала впечатление у ряда исследователей, что планирование и управление экономикой могут быть полностью осуществлены централизованно с помощью оптимизационной задачи. Леонид Витальевич. был одним из первых, кто осознал важность декомпозиционных методов и лежащих в их основе локальных решений, с помощью которых в конечном счете формируется оптимальный план для всей экономики в целом. В своих работах он постоянно указывал на использование принципов декомпозиции как при решении больших задач линейного программирования, так и при организации реального процесса составления плана. В работе <<Оптимальные модели перспективного планирования>> (1965) этот вопрос проработан им особо.

В этой, а также в ряде последующих работ Леонид Витальевич изучал вопрос построения динамической модели оптимального планирования на базе существующей статистической информации, в частности на базе информации межотраслевого баланса. Путь, указанный в этих работах, оказался плодотворным, и в свое время оптимизационные модели, базирующиеся на информации межотраслевого баланса, получили известное распространение.

В то же время внимание Л. В.  Канторовича привлекали экономические модели, которые могли быть подвергнуты достаточно полному математическому анализу в силу их малой размерности. Малоразмерные (однопродуктовые и двупродуктовые) модели довольно интенсивно исследовались за рубежом. Накоплен обширный арсенал средств анализа таких моделей. Однако Л. В.  Канторович и в этой области внес свой оригинальный вклад. В работе <<О некоторых функциональных уравнениях, возникающих при анализе однопродуктовой экономической модели>> (1959) он сформулировал такую однопродуктовую модель, в которой учитывается срок ввода основных производственных фондов. Их анализ позволяет исследовать проблему амортизации и эффективности капитальных вложений и ряд других вопросов, которые особенно актуальны именно при планировании. К изучению однопродуктовых моделей Л. В.  Канторович обращался не раз. Им рассматривались различные способы введения и учета технического прогресса. В частности, исследован вопрос о влиянии темпов технического прогресса на норматив эффективности капитальных вложений. Предложен способ оценки численной величины норматива исходя из имеющихся статистических данных. Тем самым впервые был дан объективный подход к исчислению нормы эффективности.

Экономические проблемы планирования

Л. В. Канторович внес выдающийся вклад в экономическую науку. При оценке этого вклада следует иметь в виду, что Леонид Витальевич жил и работал в стране с централизованным планированием, видел преимущества и недостатки этой системы и стремился усовершенствовать именно ее. Сделанное им не потеряло значения после изменения экономического уклада страны, хотя некоторые его достижения воспринимаются теперь в новом свете.

Рассмотрим прежде всего его вклад в проблему ценообразования - одну из коренных, затрагивающую, по существу, все сферы функционирования общества. С ликвидацией громоздкой системы централизованного установления цен научный расчет цен изменил свою роль, но не потерял значения. Принципиально важно, что Л. В. Канторович установил связь цен и общественно-необходимых затрат труда. Он дал определение понятия оптимума, оптимального развития, конкретизировав, в частности, что следует понимать под максимальным удовлетворением потребностей членов общества. Из его положения о неразрывности плана и цен вытекает зависимость общественно-необходимых затрат труда от поставленных целей общества.

Таким образом, цели общества, оптимальный план и цены составляют одно неразрывное целое. Им указаны конкретные условия, при которых объективно-обусловленные оценки оптимального плана совпадают с полными (прямыми и сопряженными) затратами труда. Определение перспектив развития экономики, наличие гигантских <<естественных монополий>> заставляет сохранить для них расчет по крайней мере опорных цен, согласованных как взаимно так и с интересами других отраслей экономики.

Математические модели получили отражение в некоторых курсах политической экономии. В работах Л. В. Канторовича исследовался ряд основных проблем экономической теории и практики хозяйствования в условиях централизованного планирования. При этом характерно, что наряду с научным, теоретическим анализом проблемы, основывающимся на единой концепции оптимального плана и оптимальных (объективно-обусловленных) оценок, Леонид Витальевич учитывал специфику проблемы, имеющийся опыт, делал конкретные выводы и давал практические предложения. Эти положения и подход нашли продолжение в работах многих ученых экономико-математического направления в нашей стране и за рубежом. В определенной, хотя к сожалению и небольшой, мере они уже используются и в экономической практике.

Указывая на недостатки действовавшей экономической системы, Л. В. Канторович подчеркивал, что система экономических показателей должна быть единой, построена по единому принципу. В связи с этим значительную часть своих работ в этой области Леонид Витальевич посвятил разработке и анализу конкретных экономических показателей.

Положение о необходимости оценки природных ресурсов и принципы такой оценки использованы в работах самого Л. В. Канторовича и его учеников. Особое внимание было уделено оценке земельных ресурсов и воды, учету этих показателей в (заготовительных) ценах на сельскохозяйственную продукцию. Предложены оригинальные подходы к их расчету (сочетание метода наименьших квадратов и линейного программирования). На этой основе были даны рекомендации по улучшению системы экономических показателей и расчетов в сельском хозяйстве. Значение предложенных им принципов расчета в складывающейся экономической системе только возрастает. Здесь достаточно указать на значение рентных платежей, например, при использовании невосполнимых ресурсов.

В работах Л. В. Канторовича вскрывается сущность понятия показателя эффективности капиталовложений, показывается его роль в экономических расчетах принятия решений, предлагается методика определения величины этого нормативного показателя. Таким образом, Л. В. Канторович дал убедительное научное обоснование необходимости применения норматива эффективности и на основе оптимизационного подхода дал объективный путь его расчета.

В работе <<Амортизационные платежи при оптимальном использовании оборудования>> (1965) Л. В. Канторовичем была вскрыта сущность понятия амортизации. Он показал, как можно повысить эффективность использования оборудования, разделив амортизационные платежи на два типа, и с помощью остроумной математической модели указал, как определить численную величину коэффициента амортизационных отчислений. Это изменение позволило сделать ряд принципиальных выводов о необходимости корректировки принятой методики расчета амортизации.

Специальный интерес Леонид Витальевич проявлял к проблемам транспорта. Еще в его первых экономических работах были даны общий анализ транспортной задачи и метод потенциалов для ее решения. Этот метод широко использовался на транспорте (железнодорожном, автомобильном, морском, воздушном) и в органах централизованного снабжения для рационального прикрепления и рациональной организации перевозок. Он безусловно сохраняет свое значение и сейчас наряду с широко используемыми сейчас методами диспетчерского управления и расчетами маршрутов.

В работах <<Об использовании математических моделей в ценообразовании на новую технику>> (1968); <<Математико-экономический анализ плановых решений и экономические условия их реализации>> (1971) Л. В. Канторович исследовал проблему эффективной работы транспорта с экономической точки зрения, показал, каковы должны быть транспортные тарифы в зависимости от вида транспорта, груза, расстояний и т. д. В ряде работ им рассматривались и вопросы комплексной транспортной системы - взаимосвязь транспорта с другими отраслями народного хозяйства и распределение перевозок между видами транспорта с учетом экономичности и в особенности энергозатрат. Эти работы сохраняют свое значение и сейчас.

В работах Л. В. Канторовича, помимо проблем народно-хозяйственного планирования, рассмотрены вопросы, относящиеся к отраслевому планированию. Наиболее простой и часто используемой является предложенная им модель, базирующаяся на транспортной задаче. На ряде более сложных моделей, в частности производственно-транспортной, динамической, декомпозиционной, им указано работах, посвященных текущему и перспективному отраслевому планированию (<<Возможности применения математических методов в вопросах производственного планирования>>, 1958) и др. Эти вопросы нашли отражение также в исследованиях отраслевых АСУ.

Большое внимание Леонид Витальевич уделял вопросам рационального использования труда. В частности, по-видимому впервые, для более рационального распределения трудовых ресурсов им было предложено введение платежей предприятий за использование труда дифференцированных по профессиям, половозрастным признакам и территории. Он указывал также на возможности научного, количественного подхода к социальным проблемам, вопросам совершенствования сферы услуг и др. Вопросы экономического стимулирования рационального использования трудовых ресурсов остаются актуальными и сейчас.

В течение ряда лет и особенно в последние годы Л. В. Канторовича интересовали проблемы эффективности технического прогресса, в частности вопросы внедрения в производство новой техники.

Особый интерес представляет обоснование предложения об установлении двух уровней цен на принципиально новую продукцию в первые годы ее выпуска. Важное значение имел также вывод об необходимости более высоко оценивать вклад в национальный доход технического прогресса и науки, чем это получалось по принятым тогда методам расчета (<<Ценообразование и технический прогресс>>, 1979).

Л. В. Канторович уделял большое внимание внедрению разработанных им методов в экономическую практику. В первую очередь в этой связи следует отметить цикл работ, посвященных методам рационального раскроя материалов, начатый Леонидом Витальевичем еще в 1939-1942 гг. В 1948-1950 гг. эти методы были внедрены на Ленинградском вагоностроительном заводе имени Егорова, на Кировском заводе и распространены впоследствии на некоторых других предприятиях. Более широкому распространению методов рационального раскроя способствовал ряд проведенных по инициативе Л. В. Канторовича совещаний.

С 1964 г. по предложению Леонида Витальевича проводилась большая работа по внедрению системных методов расчета оптимальной загрузки прокатных станов в масштабах всей страны.

Являясь членом Государственного комитета по науке и технике, Л. В. Канторович вел большую организационную работу, направленную на совершенствование методов планирования и управления народным хозяйством. Он возглавлял Научный совет ГКНТ по использованию оптимизационных расчетов, состоял членом многих ведомственных советов и комиссий (по ценообразованию, транспорту и др.). Вклад Леонида Витальевича в исследование проблемы эффективности производства и, в частности, проблемы эффективности капитальных вложений исключительно велик.

Вектор в будущее

Научная школа Л. В. Канторовича, будь то в математике или в экономике, - это не только десятки непосредственных его учеников. Это и огромное число последователей, для которых работы Л. В. Канторовича и общение с ним определили характер научного мышления и деятельности на всю жизнь.

Для своих учеников и последователей Леонид Витальевич дал образцы честности, бескомпромиссности и твердости в науке, объективности и трудолюбия. Подкупающими чертами его личности были исключительная доброта, простота и легкость общения, скромность и даже застенчивость. Он с удовольствием общался и работал с молодежью, и молодежь тянулась к нему.

Работы Леонида Витальевича Канторовича указывают нам один из путей в будущее. Мы не сомневаемся, что этот путь выберут многие.

Footnotes:

Список трудов Л. В. Канторовича опубликован в  <<Математика в СССР за сорок лет, 1917-1957>>, т. II, с. 292; <<Математика в СССР, 1958-1967>>, т. 2, вып. 1, с. 568; УМН, 1972, 27:3, с. 225;УМН, 1982, 37:3, с. 206; УМН, 1987, 42:2, с. 180-182. См. также Материалы к биобиблиографии ученых СССР. Серия математических наук, вып. 18. М.: Наука, 1986.